Longest alternating subsequence

Question

A sequence x1, x2, x3, ...,xn, is zig-zag if

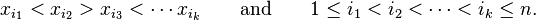
If X = 3, 4, 8, 5, 6, 2 then the length of the longest zig-zag subsequence is 5(corresponding to 3, 8, 5, 6, 2, or 4, 8, 5, 6, 2).

We define Z(i, 0) to be the EVEN length of the longest zig-zag subsequence that finishes with xi.

We define Z(i, 1) to be the ODD length of the longest zig-zag subsequence and finishes with xi.

Here's the solution recurrence:

Now my question is if there's another way to build the recurrence with the variable Z having only parameter i and incorporating 0 and 1 inside the function. If we define Z[i] to be the length of the longest zig-zag subsequence(odd or even) that finishes with xi, in what way can we express the information if z[i] is odd or even ? What would that recurrence be ?

EDIT: I worked a little bit on the recurrence and I came up with this solution. I think it is correct. Can someone else confirm ? Let's define c[i] to be the longest zigzag subsequence (odd or even) of the prefix Xi that finishes with xi. If we have only one element in the sequence then c[1] = 1 To calculate c[i] for i > 1, first we calculate the longest zigzag subsequences for (i-1) elements (both odd and even). We choose the maximum of the two and add 1. We use c[j] mod 2 == 0 controls to select only even lengths.

2 http://imageshack.com/a/img537/402/egyXmk.jpg

Answer 1

That's not possible. Whether the length of the subsequence is even or odd is an important part of information without which the formula won't work. And it can't be derived from i.