This is a similar question to this one here.
Given a list of 3D coordinates that define the surface( Point3D1, Point3D2, Point3D3, and so on), how to calculate the centroid of the surface?
In 2D the computation is given by the following formula:

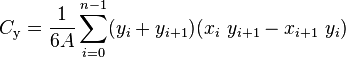
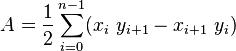
What about the 3D analogue?
The centroid (a.k.a. the center of mass, or center of gravity) of a polygon can be computed as the weighted sum of the centroids of a partition of the polygon into triangles. The centroid of a triangle is simply the average of its three vertices, i.e., it has coordinates (x1 + x2 + x3)/3 and (y1 + y2 + y3)/3.
The centroid formula is the formula used for the calculation of the centroid of a triangle. Centroid is the geometric center of any object. The centroid of a triangle refers to that point that divides the medians in 2:1. Centroid formula is given as, G = ((x1 x 1 + x2 x 2 + x3 x 3 )/3, (y1 y 1 + y2 y 2 + y3 y 3 )/3)
Just use the equations that you have twice, but the second time swap in z for y.
That is, calculate the centroids of the two projections, one onto the x-y plane, and the other onto the x-z plane. The centroids of the projections will be projections of the actual centroid, so the answer will be the x, y, and z values you find from these two calculations.
Stated more explicitly: If your points are (x1, y1, z1), (x2, y2, z2),... , to get the x-y centroid, (Cx, Cy), do a calculation using (x1, y1), (x2, y2),... and to get the x-z centroid, (Cx, Cz) use the points (x1, z1), (x2, z2),.... -- just do the second calculation with your same 2D formula, treating the z values as the y in the equation. Then your 3D centroid will be (Cx, Cy, Cz). This will work as long as your surface is flat and isn't parallel to the x-y, x-z, or y-z planes (but if it is parallel it's just the 2D equation).
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With